Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 2432
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
(For the background on this series, go here.)
On Monday, I shared an activity addressing slopes of parallel lines. Here’s the diagnosis. Here’s the original activity.
As a quick recap, this activity does a poor job with at least two principles from the Desmos Activity Building Code:
#4 – Create problematic activities.
#5 – Give students opportunities to be right and wrong in different, interesting ways.
There were three comments on Monday’s post (which is approximately three comments more than I usually get!). Go team!
Sherrina Clark suggested inquiring about students’ prior knowledge, including a concrete context, and asking students to make (and test) a prediction about what makes a pair of lines parallel.
Sam Hoggard invited me to consider the form of the equation, and whether ax + by = c might lend itself to the kind of noticing and conjecturing I’m looking for here.
Paul Jorgens reimagined the activity as a series of “finish my parallelogram” challenges. In fact, this link could be the most valuable part of this entire post. Go check it out. Right now. Seriously. I’ll hang out right here.
Okay, you’re back? Nice. Note how Paul incorporated these principles:
- Incorporate a variety of verbs and nouns. (Sketch, explain, convince, write equations, notice, imagine, etc.)
- Ask for informal analysis before formal analysis. (He asks for a sketch on Screen 1 with no grid, then adds some structure and asks for another sketch on Screen 2.)
- Give students opportunities to be right and wrong in different, interesting ways. (I am in love with Screen 8. Holy cow.)
Paul also identifies some areas for improvement, and mentions that this is a work in progress. But there’s a lot to love already.
And while I think there’s still room to grow in problematizing this task, it’s a big step up from my original activity.
My Upgrade
The best laid plans, etc. My original intention was to design and build a new version of this activity. I made it through the design stage, but only part way through building. Here goes:
Screen 1. Show students a graph of two lines. Ask them to adjust one line (using a movable point) so the lines are parallel. Then click “test it!” If the lines are parallel, they’ll never intersect, right? So I’ll find out where the lines do intersect, and zoom the window to show that point. “Bummer! Your lines intersect 103 units away from the origin,” or something like that.
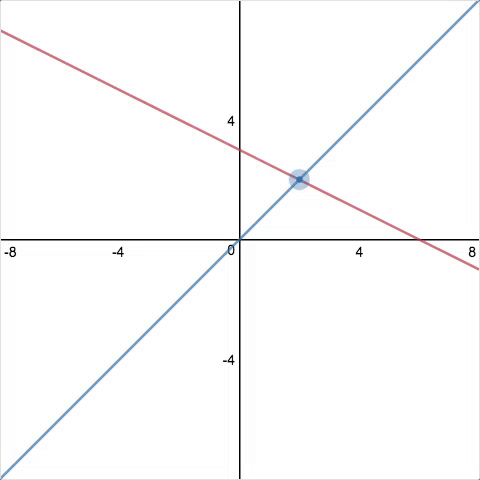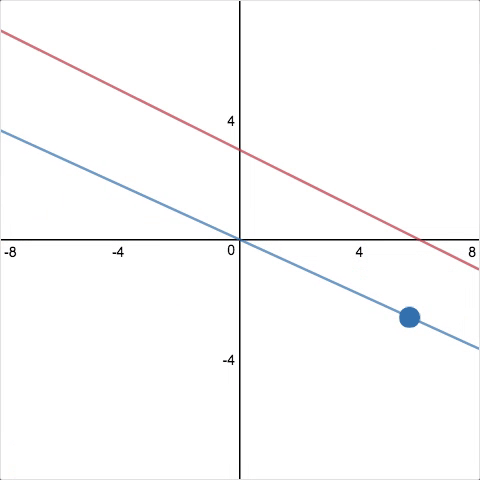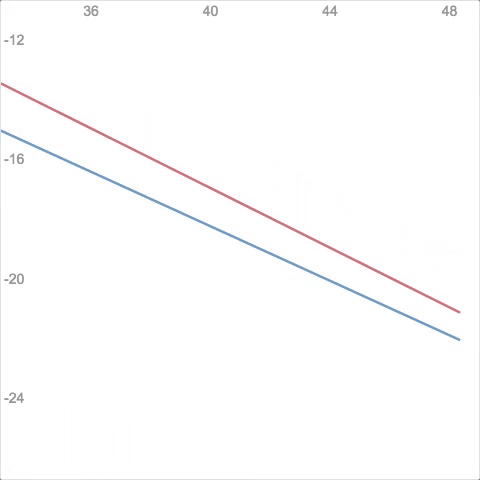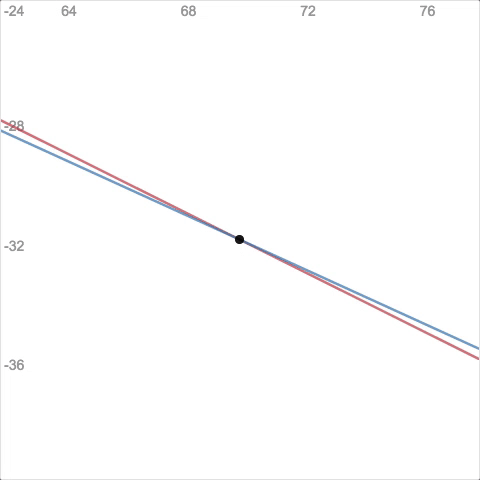
Screen 2. “Try again. Adjust your line. Really focus this time!” 🙂
Screen 3. “This is rough, right! Try just one more time.”
Screen 4. At this point, offer a lifeline. Give the same challenge, but display the equations of the lines as students tinker. My hope/anticipation here is that they’ll notice, “Hey, my lines are pretty close to parallel right now, and the equations have almost the same coefficient for x. Let’s see if I can make those coefficients exactly the same to get the lines exactly parallel!” Maybe a little optimistic? We’ll see. For what it’s worth, this would be a pretty important discussion-facilitation screen.
Screen 5. Graph screen with a multiple choice question: “Which equation has a graph PARALLEL to the line shown here?” Four options, followed by “Explain your answer.”
Screen 6. Graph screen with a math input question: “Write an equation for a line PARALLEL to such-and-such equation.” When students hit “submit,” the line appears on the graph. Feedback, but with a bit of a delay to allow room for thinking.
Screens 7-8. Same game, but with perpendicular lines. The animation would involve rotating lines, instead of zooming to the point of intersection.

Screen 9. Similar to Screen 4. Students manipulate the line, but also see the equation. (I’m still thinking through this part, to be honest.)
Screens 10-11. Multiple choice (similar to Screen 5) followed by write your own equation (similar to Screen 6).
Screen 12. Time for a card sort.

Screen 13. I’m not sure if this is an “extension,” or just a good exit ticket style question. It goes above and beyond the activity by introducing equations in various forms, so it fits the “extension” mold in my mind.

My Analysis
Principle #4 (create problematic activities): Improved. The challenge is clear from the word go: make these two lines parallel (and later, perpendicular). Is that scenario contrived? Absolutely! Did I try this with some folks after lunch today and see it quickly move into a contest of who could make their intersection point farthest from the origin? Absolutely again!
Principle #5 (give students opportunities to be right and wrong in different, interesting ways): Improved. Not perfect, by any means. But better. It’s less step-by-step, everyone do the exact same thing, and a little more free-form exploration.
Your Thoughts?
What do you like here? Where does it fall short? How could I further improve the ideas I’m exploring (or is this one destined for the trash heap)?
Let me know in the comments, or drop me a line on Twitter.
Cheers!
P.S. If you read to the end of this one, you’re a champ! Well done. 🙂
Comments 9
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Michael, I love that you’ve been so transparent and open with us about your reflection and revision process. It really helps me think about similar work I do (or need to do)… stepping back after creating, zooming out and revising initial goals and guidelines, being willing to make needed revisions…
I did preview your first version when it came out, and I really love your revisions. The traveling down the lines to see the point of intersection of *nearly* parallel lines… SO POWERFUL.
On a side note, how can I get a copy of Paul’s Parallelograms activity from teacher.desmos?
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
How did I miss this new series on Monday??? First, I just wanted to say I am always in awe of your willingness to reflect so deeply on your activities…it rubs off on me and makes me do the same with my own. I appreciate that.
Second, you took the words out of my mouth about Paul’s Screen 8…I love it!
As far as the activity goes, I think you definitely improved on the principles you were trying to achieve. On screens 1-3 I can absolutely see my kids getting excited, frustrated (in a good way), and competitive over their attempts at making the lines parallel. I can actually picture them on the edge of their seats…face inches away from the computer screen…trying every trick they can think of to get those lines exactly parallel. So good! I do wonder if it is possible to make the line exactly parallel. I also wonder if they can try more than 3 times (maybe have a reset option on the same screen instead of trying once per screen). I know “failing” 3 times will be enough motivation for some kids to be ready to move on to a more precise method of creating parallel lines, but (to paraphrase Dan Meyer) I can see some wanting more of a “headache” before they “need the asprin.” I understand the need to balance that with actually getting to the meat of the lesson, though.
I may have missed it, but is there a place students get to actually write “I noticed the slopes are parallel” and see other students’ responses so they can be sure of their thinking before moving on?
I don’t know why, but the checking for screen 7&8 throws me off a bit. Could a kid could get close enough to perpendicular that it looks correct on the screen but isn’t exactly the same line if you scrolled out? I also wonder if students would understand why the line was rotating…maybe adding in some sort of right angle arc so they can see that it’s rotating 90 degrees? I’m being a little nit picky, I think. The idea behind it is great.
I assume you’re using Desmos magic on screen 6 to make it so the line doesn’t appear until they hit a submit button…that’s cool!
For the extension, I’m not sure I would choose to have different forms of equations presented without the opportunity to play around with their graphs, first…at least not in a multiple select format.
I think there’s so much good here…definitely keep it out of the recycle bin! Can’t wait to see the end result. 🙂
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
I love this activity. I’ll try it with my students and let you know how it goes.
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Will do this just before Thanksgiving w my Geom Ss. They “discovered” parallel and perpendicular slopes during their last cycle with me. Ten days will go by before I see them again. I think it will be a FAB activity. Will let you know how they do!
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
OH! Wait. you haven’t completed it yet! I like how they have to tinker to find a line will never intersect. I am not clear how students will stumble on the perpendicular? We used card stock on lg grid paper so they knew they had perpendicular lines. How will they know if they are exactly 90 degrees from original? The card sort is yummy.
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Whitney has said it very well… Thank you, Michael, for being transparent in your thinking when designing these activities.
Part of me thinks this activity should focus solely on parallel lines, and then have a separate activity for perpendicular. But at the same time, I will also cover both concepts in the same lesson. Plus, attacking them together yields the opportunity for the card sort at the conclusion as an exit ticket. I do like how you threw that in to wrap things up. Smooth.
And I, too, would love to have a copy of Paul’s parallelogram activity. He had some very thoughtful screens.
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Hi all! Thanks for sharing your comments. 🙂
We’re waiting for another feature or two at Desmos before we can pull this off the way I want, but I’ll be sure to share the activity once it’s ready.
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Nicely done Michael! I can easily see this turning into a competition with my students.
Pingback: Parallel Lines worksheets, desmos etc – _peterprior
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371