Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 2432
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
My polar graphing unit in Precalculus has always started in the same lackluster way: With me telling students how to graph polar coordinates. We then launch into some point-by-point graphing, followed by various explorations and challenges involving graphing polar equations, and we’re off to the races.
This year I wanted to try something different. Instead of telling students how to plot polar coordinates, I wanted them to discover the mechanics by using technology to plot a handful of points.
It wasn’t exactly profound, but this brief introductory lesson felt like an improvement. I started by displaying these images:
We then fired up Desmos, with students working in pairs. Once everyone successfully plotted the first point, I turned them loose on this:
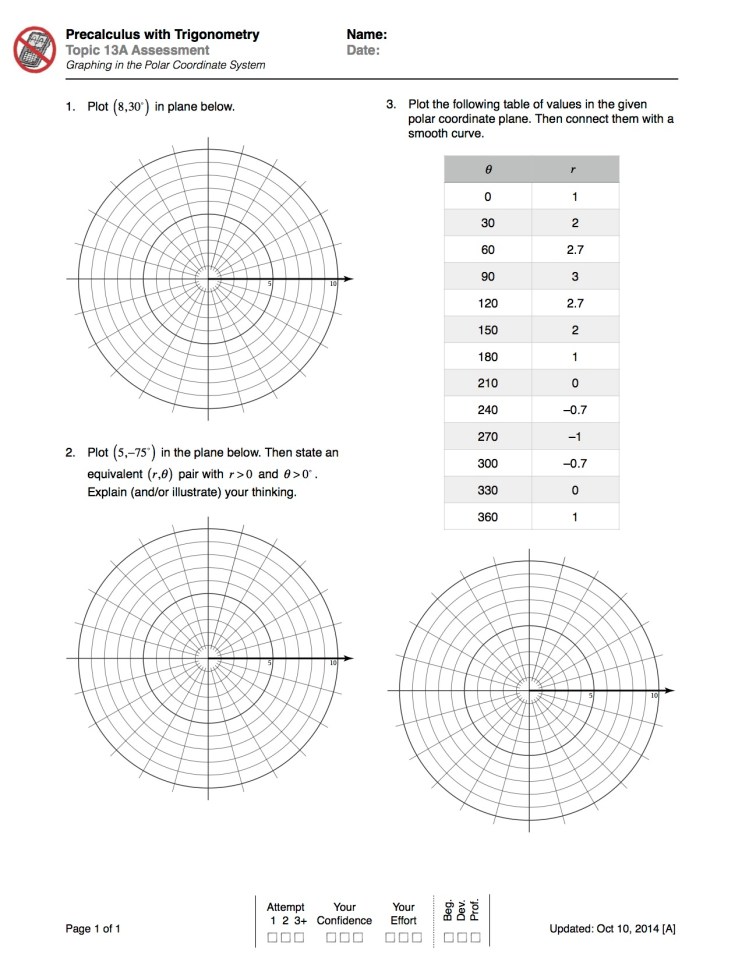
That’s my “can you plot points in the polar coordinate plane” assessment from last year. I don’t allow students to use a calculator on it, at least not when it’s a real assessment. As a learning tool, especially without the usual direct instruction intro, this page paired nicely with a bit of technology.
Debriefing
My favorite part from this brief lesson came at the end when we discussed what to do with negative radii and/or negative angles. In the past, it was a lot of “do this” and “do that” and “don’t forget this.” Here, I invited students to share their observations and make conjectures about points involving negative values.
And the payoff was in what happened next: Instead of “yes, that’s right” or “nope, try again” from me as the expert, we turned back to Desmos to test (and in most cases refine) our conjectures. While there’s still some learning to be done here, I think we’re got off to a decent start.
Looking Ahead
Next up, in reality: A Desmos-driven, noticing-and-wondering exploration with six types of polar equations. If all goes according to plan, I’ll blog about it soon.
Next up, in my ideal world: In the future, I’d prefer to squeeze an extra lesson in prior to the aforementioned/upcoming exploration. This in-between lesson would involve each student receiving an equation, finding its value every 10 degrees (from 0 to 360), and plotting those points by hand on a polar grid. I think this would serve as a nice link between the “hey, now I can graph polar points!” lesson described above, and the “oh, sweet! Desmos can graph these equations in milliseconds” exploration that follows. Maybe next time…




Comments 6
Pingback: Polar Graphing Exploration | Reason and Wonder
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Question I’ve never thought to ask. Why polar coordinates? What itch does that scratch? Best I have is that some of these polar functions which are quite simple to write in polar notation would be a pain in the ass in their Cartesian form. Is there something else I’m missing, though?
In general: I’m curious why we invented so many different notations to represent a point in space.
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Just a quick thought… Maybe because they are functions this way… Also lots of things rotate.
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Dan, I know the standard answer for this and other questions is usually to point to applications (http://en.wikipedia.org/wiki/Polar_coordinate_system#Applications). And I know this is relevant to some people, either personally (interest) or professionally. But I don’t teach polar coordinates to scratch the applications itch, and none of my students have ever seemed particularly inspired by my references to applications (which I do make).
For me, this is simply another mathematical playground for developing the things I care most about. I want my students to make connections and develop habits-of-mind/SMP-style things. I can’t tell if this is the world’s most epic motivational cop-out, or if it’s a healthy standard measure of whether something is worth teaching: “Does this give students an opportunity to grow in (fill-in-the-blank-meaningful-way)?”
Regarding why we invented so many different notations, I’d offer: Someone at some point found it more efficient/effective/powerful/simple to represent something in another way. So he/she did. End of (that) story.
The next story (and the one I’m more interested in) is how we decide which notations/representations (whether of points in space, or some other topic) are worth bringing before our students. There are plenty of “useful” things (from an applications standpoint) that we leave out of the classroom. What makes the canon? What doesn’t? And why?
P.S. If I took my response-rant in another direction, I’d be all over Kaleb’s rotation angle. And probably would have mentioned a few things Michael Pershan has said about complex numbers and transformations. But to me, some of that is a means to an end, and the end is not navigating an airplane more effectively. I think. 🙂
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
My husband was in the Marine Corps. In his early training, he was dropped off in the middle of a forest and had to find his way out. He was given a map and a compass. He used the heading and paces to get from one point to another. (polar coordinates). When he was a pilot, polar coordinates again in a sense because he had to fly from one point to the next knowing heading and distance.
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Author
Cinda,
Thanks for the comment, and the two great applications!
Take care,
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371