Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 2432
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Most of the work my students do with Visual Patterns occurs in small groups, where collaboration not only is encouraged, but often required. Today I steered things in a slightly different direction.

I wanted to see what students were capable of on their own. No peer discussion. No Desmos. I was particularly interested to see whether they could write an equation to describe the relationship they see unfolding visually, numerically, and graphically. Some could. Some could not.
As I walked throughout the room, I took note of the incorrect equations students were writing down. There were four in particular that caught my eye. Students were clearly doing some relevant work with calculating slope and (trying, anyway) to identify the y-intercept… However, the way they mashed it all together left something to be desired.
On the Fly…
So as my last few students were finishing their work, I threw together this slide, featuring the pattern they had been working with, four “out-in-the-wild” incorrect equations, and a not-so-accidental suggestion that one of the equations is correct (just to keep ’em on their toes):
We then took a blank sheet of printer paper, folded it in half, and unfolded it. Two workspaces on the front, and two on the back. We then filled each workspace with an equation as well as a table of the actual values…
…plus a show-your-thinking-on-the-page run through of each x-value, evaluated in the given equation.
In each case, the expression values didn’t match the actual values, and the equation proved to be an imposter. While this “let’s evaluate” approach was rather typical, and the discussion was somewhat predictable, the results were nevertheless quite powerful. The major issues we identified and addressed were:
- Students lacked a go-to strategy for verifying whether their equation was valid. It’s almost as if they viewed the progression (from numerical to algebraic) as a one-way street. Our conversation helped them see how to go from numerical to algebraic, and then back again to confirm. I probably should have equipped them with this skill some time ago. Better late than never.
- Students were working with some faulty y-intercept assumptions. The evidence suggests (and their comments confirm) that of those who got this wrong, most went hunting for the y-intercept where it’s often found: at the top of the table. “The y-intercept occurs when the x-value is zero…” is not something that has stuck with them, despite visual, verbal, and numerical attempts to drive that home. I’m cautiously optimistic that today’s conversation smashed that misconception for most students.
Side Benefit
While most students wrote an equation with a rate of change of 4 new circles per stage, I did have a few “slope stragglers” suggest equations like y = x + 4 and y = 10x + 4. As we evaluated multiple x-values in each of four equations, and left a record of our evaluating on the board, the similarities and differences rose to the surface. The connection between the coefficients of our faulty equations (1, 4, 4, and 10) and the common differences between expression results caused a few more light bulbs to turn on.
Future Use
We’ll continue to explore Visual Patterns in small groups most the time, but I think I’ll include a dose of individual formative assessment, followed by small-group or whole-class error analysis now and again. We unpacked a lot of misconceptions today, and made a number of valuable connections as well, all in a rather short period of time. Anything that draws out misconceptions so we can smash ’em to bits through class discussion is worth bringing back for an encore.



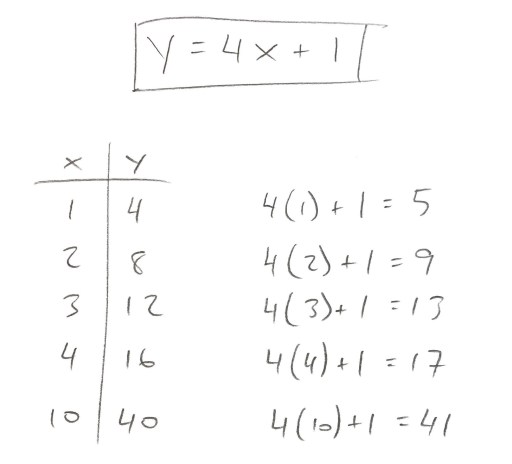
Comments 1
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
A couple of comments. 1) I teach Precalculus and many of my students STILL can’t seem to remember that the y-intercept is when x = 0 either, despite much repetition. 2) I, too, encourage group work, but have recently realized that some students, although they were engaged and contributing greatly in group work, were still not fully mastering concepts because they were too dependent on others to do part of the thinking for them. I counseled certain students NOT to study with other students when preparing for a test so that they could learn things for themselves.
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371