Reason and Wonder

Charge! v2 – Activity Makeover

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 2432

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Background. I’ll share an activity. Offer some ideas on what’s wrong. Invite you to share your own diagnosis/treatment. Then (end of week) share an upgraded version of the activity. (More details about this series are available here.)

Several Mondays ago, I shared the Desmos Activity Builder version of Charge!, a linear modeling task where students predict how long it will take for a phone to become fully charged. Here’s the diagnosis.

In that post I suggested that the Activity Builder version of this activity was inferior to its original slide-deck-driven version, in part because it struggles with these principles from the Desmos activity building code:

#5 – Give students opportunities to be right and wrong in different, interesting ways.
#8 – Create objects that promote mathematical conversations between teachers and students.

Featured Comments

Dave Johnston: “Can we give students more chucks of the data and give them an opportunity to revise their model? What if different groups of students had different data points along the way & they discussed the models they came up with?”

Nathan Kraft: “I’m trying to figure out what Desmos adds to the activity… This activity pigeonholes students into one way of doing it, and even for students in higher grades, I’d like to give that option to explore it differently… In the end, maybe this doesn’t work in activity builder.”

Elizabeth Raskin: “One of the beautiful things about 3 acts is allowing students to determine what information is important (to an extent) and what to do with it.”

Mark Kreie: “Utilizing the Classroom Conversation Toolkit w/ teacher pacing and pausing might be a benefit to this activity.”

My Upgrade

I find myself wondering what several commenters suggested: maybe the best version of this task doesn’t live in Activity Builder. I’m definitely open to that possibility.

That being said, I still wanted to see how far forward I could push the AB version.

I recommend opening up Charge! v2 while you read through the rest of the post. Here is what’s new:

Fresh artwork, all throughout, including a video reveal. This doesn’t shift the pedagogy, or address the weaknesses above, but it adds a little polish to the existing structure. And when it comes to the video, that adds a little anticipation, which is often a good thing in a math classroom.
Condensed opening. I love asking students “what do you notice/wonder?” But I haven’t figured out how to open an Activity Builder activity with that approach. So I’ve trimmed the opening to make room for more discussion later on, a la Principle #8 (“Create objects that promote conversations…”).
“Informalized” the sketch on Screen 2. Goodbye axis scale. Goodbye grid. Goodbye sample data points. Hello increased variety of student responses. That’s the plan, anyway. I’m anticipating an uptick in variety here, ranging from type of graph (linear vs nonlinear) to features of specific sketches (e.g., steepness, starting point). And that could lead to some nice interplay between Principle #5 and Principle #8.
Condensed middle. The core here is much tighter. It’s now: Build a model. Use the model. Interpret your model. This condensing improves our conversation-to-screen ratio, which has been a theme around Desmos HQ for the past few months. For so many activities—this one included—carving out time to explore what they’ve done on each screen is crucial. There just isn’t enough time to do a 20-screen activity and discuss it. By cutting the screen count in half (from 18 to 9), I’m hopeful that there’s sufficient room for those important discussions to unfold.
Different ending. I pulled the “why do you think it charged that way” question forward to the new Screen 8, which makes room for a new extension on Screen 9. Note two differences: (1) the phone is different, and (2) the direction of the question is different. Instead of “given the charge, what is the time,” it’s reversed: “given the time, what is the charge?”

(Pssst. Did you see that video reveal?)

Lingering Concerns

Is v2 better than v1? In my opinion, absolutely. Is v2 perfect? Not even close.

I think this new version better addresses Principle #8 (“Create objects that promote conversations…”). Fewer screens. More room for conversation.

But I don’t think I’ve addressed the more difficult Principle #5: “Give students opportunities to be right and wrong in different, interesting ways.”

There’s still just one way to move through this activity. It still feels too scripted. Maybe it does live best outside of Activity Builder. Or maybe not. I’ll continue thinking and tinkering. Hopefully most of my steps are forward.

Invitation

What do you think of the upgrade? Which of the featured comments resonated with you? What could be done to better address Principle #5?

Let me know in the comments, or drop me a line on Twitter.

Cheers!

LEGO Prices vs Marriage Age – Contrasting Activities

I spend a fair amount of my time at Desmos creating activities with the Activity Builder. In my mind, the job becomes more and more interesting over time for at least two key reasons:

Over time, the toolset expands.
Over time, our sense of how to use the toolset expands. That is, our pedagogy improves.

These two developments play off one another, and we find ourselves with more and more opportunities to build increasingly interesting things.

One way we push our pedagogy forward is by holding up two activities and asking questions like:

How are they similar? How are they different?
What are their strengths? What are their weaknesses?
In what ways could the Activity Building Code inform these activities? In what ways could these activities inform the building code?

Recent Comparison

Earlier this week, we took a close look at two linear modeling activities: LEGO Prices and Are People Waiting to Get Married?

If you’re up for it, I’d love to hear your analysis (similarities/differences, strengths/weakness, relationship to the building code) in the comments.

My Thoughts

Each activity has its own strengths, and each activity has the potential to generate interesting class discussion. However, I think LEGO Prices does a much better job with creating problematic activities (Principle #4 if you’re counting).

Are People Waiting to Get Married? nibbles at the edges of a context in a largely disconnected way.

Students make a prediction, but it never resurfaces.
Students sketch on a graph, but we’re not told why.
Students make another prediction, but that too never resurfaces.
Students write equations. Why? Because we tell them to.

LEGO Prices hits you right out of the gate with a single, overarching question that will drive the rest of the activity: How much did that LEGO set cost?!

Students make a prediction, and it resurfaces later in order to compare the power of wild guesses with the power of mathematics.
Students sketch in order to better understand the relationship.
Students build and then use a model in order to refine their prediction.

The key phrase for me here is in order to. That’s the difference. As much as Are People Waiting… has going for it (and, by the way, I rather love Screen 8), there’s no in order to attached to the tasks we’ve given students. Instead, it’s piecemeal. Screen-by-screen. Asking because we can, not because we must. Questions that serve themselves, rather than a single, coherent pursuit.

LEGO Prices suffers in other ways. For example, I think it does a fairly awful job with Principle #5: “Give students opportunities to be right and wrong in different, interesting ways.” It’s narrow-minded in that sense. There’s really just one way to move through the activity. I’m discouraged by that, and hope to discover creative solutions around that weakness in future activities.

And yet while it struggles with that, it doesn’t struggle with this: clarity of purpose. With the exception of Screen 5 (interpreting parameters), everything students do is done in the service of making the most insightful and accurate price prediction they can.

And that’s something I’ll be trying to infuse in similar tasks in the future.

Invitation

What did you see in the activities? What did you think of my analysis? Where did it resonate? Where do you think it’s off base? I’d love to hear your thoughts in the comments.

Cheers!

CMC North 2016

Math teachers are amazing.

Exhibit A: Last weekend I spent an hour with a group of math teachers who woke up early on a Saturday morning to hone their craft. We were just steps away from the beach in Monterey, and yet they’re willing—hungry, even—to gather in a room to reflect on their own learning and teaching, even at 8 am. That’s just awesome.

Snapshot

If you weren’t able to join us, here’s a quick snapshot of the session:

Some of the ways we use technology in the math classroom waste the human potential in the room. Picture computer cubicles. Kiddos wearing headphones. Teachers grading papers while students work in isolation.
Let’s build something better. Let’s build activities—digital or otherwise—that spark more conversation, more discussion, more human engagement. And let’s build tools to help teachers facilitate those activities more effectively.
With that in mind, the team at Desmos built a Classroom Conversation Toolset. You can read about it here.
We’ve also spent considerable time thinking about the strengths and weaknesses of the activities we’ve built over the last year or so, and codified those thoughts into our Activity Building Code. You can read about it here.

Activities + Principles

Here’s a list of the activities we looked at during the session, along with the principles I had in mind for each one:

Graphs of Lines. Create objects that promote mathematical conversations between teachers and students.
The Intersection. Create an intellectual need for new mathematical skills.
Point Collector. Create activities that are easy to start, difficult to finish.
Function Carnival. Connect representations.
Marbleslides: Lines. Integrate strategy and practice.

My hope is that these activities serve as exemplars for the principles, and that folks in the session walked away with a sense of how the principles might apply in other situations (whether Desmos or non-Desmos, digital or non-digital). We ended with a brief quiz to encourage folks to wrestle with these principles in new contexts.

Quiz

Here’s the quiz. Take a look at each task, and let me know in the comments which principle(s) you think each activity exemplifies.

(To check your answers, turn the cereal box upside down. Wait, no. That’s something else. Never mind.)

Slides

The original presentation included quite a lot of video (to quickly show off the activities linked above), as well as a presenter (hi there!). So this version of the slide deck (which includes neither) may not be very helpful. But, in case it is, you can download it here.

Charge! – Activity Makeover Series

Activity and Diagnosis

A couple years ago, I sat against the wall in my sons’ bedroom, taking screenshots of my smartphone once every four minutes for an entire evening. (Why, you ask? For math!)

The result: Charge! (quite likely my only decent entry into the world of three act tasks).

About a year ago, I created an Activity Builder version of the task. And I’ve never been satisfied with it.

I think it’s better than nothing at all, but undeniably worse than the slide-driven, conversation-rich, paper-and-pencil version I posted on my blog a while back.

When it comes to the Desmos activity building code, this activity—even in its AB-powered form—succeeds on several fronts, including “create problematic activities” and “connect representations” (among others).

However, it struggles in ways that overshadow its strengths. Most notably:

#5 – Give students opportunities to be right and wrong in different, interesting ways. The AB version of Charge! feels too scripted. Too narrow. Rather uninteresting. “Do this. Now this. Next, this. Now do this.” And so on, all the way through the activity. There’s really just one path, and the activity leads students along it with minimal opportunity (or even need) for careful reflection or critical thought.

#8 – Create objects that promote mathematical conversations between teachers and students. This is a tricky one. I believe the activity could generate classroom discussion, but that the sheer number of screens works against that possibility, rather than in support of it. Let’s assume a 50-minute class period, with 45-minutes dedicated to this activity. That’s just 2.5 minutes per screen, which isn’t terribly conducive to classroom discussions. It might be wise to trim the number of screens so that there’s room for deeper discussions on a smaller set of screens.

#13 – Ask proxy questions. Would I recommend this activity? Nope. Not in its current form. I’d be much more comfortable recommending the original slide-based version. With the activity parsed into 18 step-by-step style screens, there’s no one screen with anything really interesting happening on it. One of my colleagues likes to consider the quality of an activity by asking whether any of the work students do on a given screen could be considered fridge-worthy. In other words, if they could print it out and take it home to show mom and dad, would it end up on the fridge as a proud display of something deep or delightful? Again, because I’ve chopped the interesting work in Charge! into 18 tiny bits, the answer is no. Nothing fridge-worthy in this approach.

Invitation

Will you offer your own diagnosis? A second opinion of sorts? What do you think is wrong with this activity?
Better yet, will you offer suggestions for your own treatment? How would you make this activity better?
Better still, will you build and share a new, better activity that addresses the shortcomings identified in one of the diagnoses?

Drop a line (or two) in the comments, or let me know what you think on Twitter (@mjfenton).

I’ll be back Friday with a new treatment of my own.

Cheers!

Parallel Lines v2 – Activity Makeover Series

(For the background on this series, go here.)

On Monday, I shared an activity addressing slopes of parallel lines. Here’s the diagnosis. Here’s the original activity.

As a quick recap, this activity does a poor job with at least two principles from the Desmos Activity Building Code:

#4 – Create problematic activities.

#5 – Give students opportunities to be right and wrong in different, interesting ways.

There were three comments on Monday’s post (which is approximately three comments more than I usually get!). Go team!

Sherrina Clark suggested inquiring about students’ prior knowledge, including a concrete context, and asking students to make (and test) a prediction about what makes a pair of lines parallel.

Sam Hoggard invited me to consider the form of the equation, and whether ax + by = c might lend itself to the kind of noticing and conjecturing I’m looking for here.

Paul Jorgens reimagined the activity as a series of “finish my parallelogram” challenges. In fact, this link could be the most valuable part of this entire post. Go check it out. Right now. Seriously. I’ll hang out right here.

Okay, you’re back? Nice. Note how Paul incorporated these principles:

Incorporate a variety of verbs and nouns. (Sketch, explain, convince, write equations, notice, imagine, etc.)
Ask for informal analysis before formal analysis. (He asks for a sketch on Screen 1 with no grid, then adds some structure and asks for another sketch on Screen 2.)
Give students opportunities to be right and wrong in different, interesting ways. (I am in love with Screen 8. Holy cow.)

Paul also identifies some areas for improvement, and mentions that this is a work in progress. But there’s a lot to love already.

And while I think there’s still room to grow in problematizing this task, it’s a big step up from my original activity.

My Upgrade

The best laid plans, etc. My original intention was to design and build a new version of this activity. I made it through the design stage, but only part way through building. Here goes:

Screen 1. Show students a graph of two lines. Ask them to adjust one line (using a movable point) so the lines are parallel. Then click “test it!” If the lines are parallel, they’ll never intersect, right? So I’ll find out where the lines do intersect, and zoom the window to show that point. “Bummer! Your lines intersect 103 units away from the origin,” or something like that.

Screen 2. “Try again. Adjust your line. Really focus this time!” 🙂

Screen 3. “This is rough, right! Try just one more time.”

Screen 4. At this point, offer a lifeline. Give the same challenge, but display the equations of the lines as students tinker. My hope/anticipation here is that they’ll notice, “Hey, my lines are pretty close to parallel right now, and the equations have almost the same coefficient for x. Let’s see if I can make those coefficients exactly the same to get the lines exactly parallel!” Maybe a little optimistic? We’ll see. For what it’s worth, this would be a pretty important discussion-facilitation screen.

Screen 5. Graph screen with a multiple choice question: “Which equation has a graph PARALLEL to the line shown here?” Four options, followed by “Explain your answer.”

Screen 6. Graph screen with a math input question: “Write an equation for a line PARALLEL to such-and-such equation.” When students hit “submit,” the line appears on the graph. Feedback, but with a bit of a delay to allow room for thinking.

Screens 7-8. Same game, but with perpendicular lines. The animation would involve rotating lines, instead of zooming to the point of intersection.

Screen 9. Similar to Screen 4. Students manipulate the line, but also see the equation. (I’m still thinking through this part, to be honest.)

Screens 10-11. Multiple choice (similar to Screen 5) followed by write your own equation (similar to Screen 6).

Screen 12. Time for a card sort.

Screen 13. I’m not sure if this is an “extension,” or just a good exit ticket style question. It goes above and beyond the activity by introducing equations in various forms, so it fits the “extension” mold in my mind.

My Analysis

Principle #4 (create problematic activities): Improved. The challenge is clear from the word go: make these two lines parallel (and later, perpendicular). Is that scenario contrived? Absolutely! Did I try this with some folks after lunch today and see it quickly move into a contest of who could make their intersection point farthest from the origin? Absolutely again!

Principle #5 (give students opportunities to be right and wrong in different, interesting ways): Improved. Not perfect, by any means. But better. It’s less step-by-step, everyone do the exact same thing, and a little more free-form exploration.

Your Thoughts?

What do you like here? Where does it fall short? How could I further improve the ideas I’m exploring (or is this one destined for the trash heap)?

Let me know in the comments, or drop me a line on Twitter.

Cheers!

P.S. If you read to the end of this one, you’re a champ! Well done. 🙂

Parallel Lines – Activity Makeover Series

Activity and Diagnosis

Some months back, I wrote an activity called Parallel Lines. Here’s the description:

“In this activity, students explore connections between the graphs and equations of parallel lines.”

It’s not awful. But it’s far from great. It really struggles with two principles of our building code in particular:

#4 – Create problematic activities. It’s not clear to students what they’re doing—or why they’re doing it—until the end of the activity (or maybe even at all).

#5 – Give students opportunities to be right and wrong in different, interesting ways. There’s really just one correct path through this thing. And I don’t believe there are interesting ways to be wrong here, either. Bottom line: expect a lot of similar, uninteresting student responses. I’m not sure that’s the best fodder for rich classroom discussion.

Invitation

Will you offer your own diagnosis? A second opinion of sorts? What do you think is wrong with this activity?
Better yet, will you offer suggestions for your own treatment? How would you make this activity better?
Better still, will you build and share a new, better activity that addresses the shortcomings identified in one of the diagnoses?

Drop a line (or two) in the comments, or let me know what you think on Twitter (@mjfenton).

I’ll be back Friday with a new treatment of my own.

Cheers!

Diagnosis and Treatment – Activity Makeover Series

Last week I gave a talk at CMC South called Principles for Building and Using Effective Digital Tasks.

For the “building” piece, I shared five principles from the Desmos Activity Building Code. For each principle, I offered an exemplar activity.

In one case, I even offered an anti-exemplar. I find these contrasts between what works and what doesn’t particularly helpful for developing my own capacity to build more of what works.

With that in mind, I’m kicking off a new series here.

Every Monday, I’ll post an activity that fails to live up to the building code in some way. I’ll share one or two shortcomings that I see. In short, I’ll offer my diagnosis.

Every Friday, I’ll post an upgraded version of the activity, with some commentary on the changes I made. In short, I’ll share my treatment.

And that cycle will be helpful, at least for me. The process of select/reflect/revise/explain will gradually boost my activity building skills.

But! What happens between Monday and Friday, that’s where this could get really interesting.

Will you offer your own diagnosis? A second opinion of sorts?
Better yet, will you offer suggestions for your own treatment?
Better still, will you build and share a new, better activity that addresses the shortcomings identified in one of the diagnoses?

Whatever level of participation you choose, I do hope you’ll join in the fun.

Keep your eyes on this space. The first activity + diagnosis is coming soon.

Cheers!

Transformative Principal Podcast Appearance

A few weeks ago I had a conversation about what’s new and exciting in the world of Desmos with Jethro Jones, the principal of Kodiak Middle School in Kodiak, Alaska.

He recently posted our conversation (in two parts) on his podcast, Transformative Principal.

If you’re into that sort of thing, you can listen in here: Part 1 and Part 2

Enjoy!

ZPC Podcast Appearance

Earlier this week I gave a talk at the AIMS Center on using Desmos to facilitate classroom discussion around digital activities. While on campus, I stopped by their podcast booth for a 20-minute conversation with Chris Brownell.

Dr. Brownell is the Director of Mathematics and STEM Education Programs at Fresno Pacific University—home of the AIMS Center—and also the host of the podcast Zone of Potential Construction. (He’s also a former instructor of mine.)

If you’re interested, you can listen to the podcast here.

You can also subscribe to the podcast. Just search for “zone of potential construction” in your favorite podcast app.

WNBA Scoring Averages – Activity Analysis

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Warning: count(): Parameter must be an array or an object that implements Countable in /home3/reasonan/public_html/wp-includes/media.php on line 1206

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 2432

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371

Here’s an image from an activity (WNBA Scoring Averages) that I wrote earlier this year.

When we dropped the activity into the search pool at teacher.desmos.com, I didn’t think it was a world-changer, but I was pretty sure it wasn’t untouchably awful.

Hang on a sec while I fire up our database to check how many times it’s been run since it arrived on the scene in May 2016 .

Seven, eight, carry the one… Round up for good measure… Almost there… Aaaaaand…

Zero. Zero sessions.

Needless to say, that’s not a lot of sessions.

So what went wrong? I’ll offer a few theories, and along the way highlight a couple of things that might be worth preserving. I’d also love to hear your thoughts on how to make this—and activities like it—better.

Screens 1-3

Bummer. 27% of the activity just to set the context. That’s killing my discussion-to-screen-count ratio.

Screen 3 (above)

Before asking for a calculation, ask for a prediction. Nice!

Screen 4

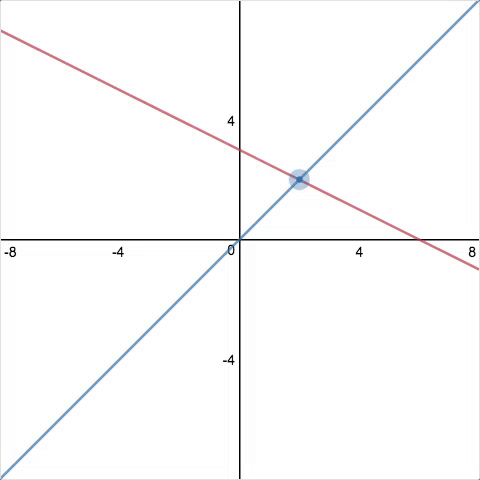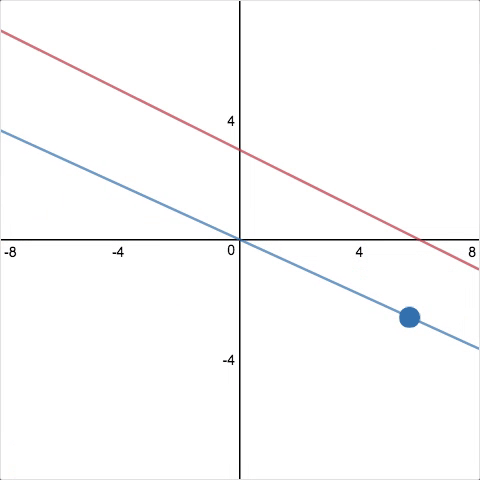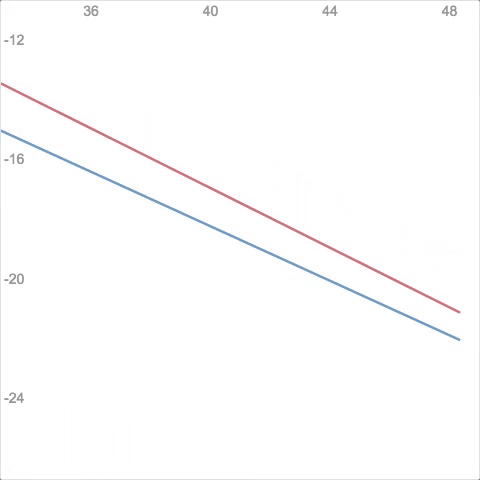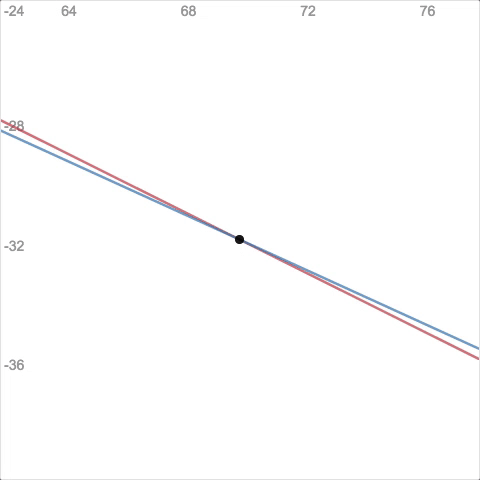
An opportunity for students to wrestle with the meaning of a scatterplot in a setting they haven’t seen a thousand times. Also, a chance for teachers to highlight interesting responses, starting with informal ones and progressing to formal ones. That being said, I can’t shake the feeling that nobody cares about the patterns they see on this screen.

Screen 5

This screen’s a mess. “The red point means WHAT? My original prediction? I can’t remember that!” And a purple point that I might move? This is just awful. (P.S. What’s the input field for on this screen?)

Screen 6

I can just hear the conversation now… Me: “In row 1, write the equation…” Students: “Why?” Me: “Because I said so.” That line hasn’t been working with my three year old twins at bedtime, and I don’t think it’s going to play out well in the classroom. There’s got to be a better motivation for plotting this line now, something beyond the “trust me, just do it” rationale I offer here. Maybe the solution is to skip having students enter the line, and just jump from Screen 5 to 7?

Screen 7

Continuing that thought… I propose deleting Screen 6, and revising Screen 7 to read: “(1) How do the points compare to the line y = x (shown in black)? (2) What does this mean in context?” Even still, I’m not sure how strong a screen that leaves us with.

Screen 8

“Boom, a line of fit! Now use it! ” This screen reveals a couple of major open question I have about modeling activities in Desmos Activity Builder. (1) Should students generate the line or curve of fit? Always? Sometimes? Never? I think “sometimes” is the right answer here. But I’m not clear (yet) on when it’s the right move. Here I offer it to students “for free” so they can focus on using and interpreting the line. But I’m not sure that’s the right move. (2) Many of the modeling tasks I’ve build in Activity Builder feel a little too linear and granular (as in, one tiny step, then the next tiny step, and another, and another, with all students moving through in the more or less the same manner and sequence). Is this the best approach? I doubt it. But what’s the alternative? I haven’t figured that out yet.

Screen 9

Interpret the parameters in context. Yay!? But—students had no role in generating that value, so it feels uninteresting to ask about it. I’m wondering about an alternative screen—or sequence of screens—where students use sliders to create their own line of fit. Then answer a question or two about the meaning of their parameters in context, ideally in contrast to a classmates’ parameters. Hm. Still feels lackluster.

Screen 10

I’ve thrown this discussion-prompting screen into a handful of activities over the last several months. Do you think it’s helpful? My hunch is that some teacher tips go unread, but a student-facing screen encouraging discussion at this point is sure to be noticed.

Screen 11

As was shared recently over on the Desmos blog, we strive to activities that are easy to start and difficult to finish. Low floor, high ceiling, etc. Extension screens are one small part of that puzzle, and I’ve dropped one in here to wring a little more value out of the context, and to spark (possibly) a conversation about residuals. I like this screen. At least I think so. I’d love to know what you think.

General

I’ve rambled a bit about what I do like, and what I don’t like. And in the latter, hinted at ways that I might be able to improve this activity. Unfortunately, even with those improvements, I don’t think this is a particularly strong activity. It lacks a compelling problem. There’s very little cognitive conflict, even with the predictions at the beginning. (Maybe I could hold those up at some point early on: “Here’s your prediction. Here’s all your classmates’ predictions. Let’s see who’s closest!” Or maybe not.) Students don’t have very many opportunities (if any) to be right or wrong in interesting ways.

Over To You

So what do you think? Is this salvageable? What does it suffer from in its current form? What strengths does it have, and how could we build on those?

Thanks in advance for chiming in!

Page 2 of 16
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
←

Deprecated

/home3/reasonan/public_html/wp-includes/formatting.php

4371

Deprecated

/home3/reasonan/public_html/wp-includes/formatting.php

4371

Deprecated

/home3/reasonan/public_html/wp-includes/formatting.php

4371

16
Deprecated: Function get_magic_quotes_gpc() is deprecated in /home3/reasonan/public_html/wp-includes/formatting.php on line 4371
→